hanvova.blogg.se - Isosceles triangle sides are equal

#ISOSCELES TRIANGLE SIDES ARE EQUAL TRIAL#
#ISOSCELES TRIANGLE SIDES ARE EQUAL FREE#

Similarly, the side opposite to the largest interior angle is the longest side and vice versa.

The side opposite to the smallest interior angle is the shortest side and vice versa.

Similarly, the difference between the lengths of any two sides of a triangle is always less than the length of the third side.

The sum of the lengths of any two sides of a triangle is always greater than the length of the third side.

An exterior angle of a triangle is equal to the sum of its two interior opposite angles.

The sum of all exterior angles of any triangle is equal to 360°.

The sum of all interior angles of any triangle is equal to 180°.

Let us summarize some of the important properties of a triangle. Properties of Triangle: Summary & Key Takeaways

Area of a right-angled triangle = ½ * product of the two perpendicular sides.

Area of any triangle = ½ * base * height.

This is a scalene right-angled triangle since all three angles are different.

The sides opposite to these angles will be in the ratio – 1: √3: 2 respectively.

The angles of this triangle are in the ratio – 1: 2: 3, and.

This is a right-angled triangle, since one angle = 90°.

This is also called an isosceles right-angled triangle since two angles are equal.

The sides of this triangle will be in the ratio – 1: 1: √2 respectively.

Two angles measure 45°, and the third angle is a right angle.

Let’s also see a few special cases of a right-angled triangle 45-45-90 triangle

#ISOSCELES TRIANGLE SIDES ARE EQUAL FREE#

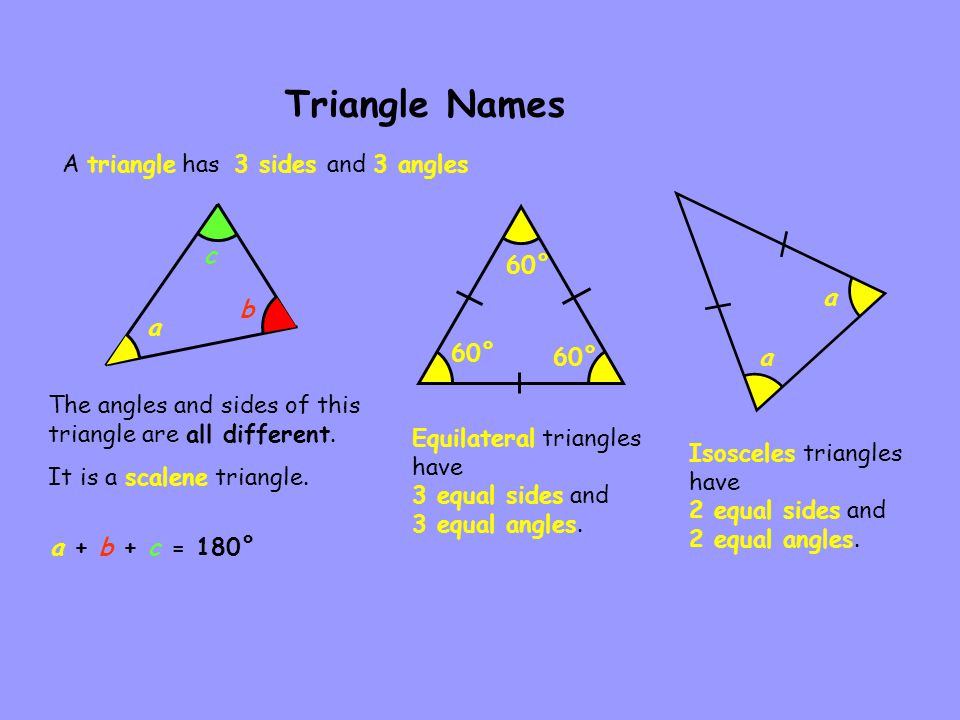
Take a free mock Special cases of Right Angle Triangles | Special properties of Triangle Each interior angle of an equilateral triangle = 60°.Since all the three sides are of the same length, all the three angles will also be equal.Equilateral triangle | Properties of TriangleĪ triangle that has all three sides of the same length is an equilateral triangle. Given below is an example of an isosceles triangle. The angles opposite the equal sides measure the same.Given below is an example of a scalene triangle Isosceles triangleĪ triangle that has two sides of the same length and the third side of a different length is an isosceles triangle. Since all the three sides are of different lengths, the three angles will also be different.We are the most reviewed online GMAT Prep company with 2500+ reviews on GMATClub.Ĭreate your Personalized Study Plan Scalene triangleĪ triangle that has all three sides of different lengths is a scalene triangle.

#ISOSCELES TRIANGLE SIDES ARE EQUAL TRIAL#

Ace GMAT Quant by signing up for our free trial and get access to 400+ questions. Questions on triangles are very commonly asked on the GMAT. Given below is an example of an obtuse/oblique angle triangle. Obtuse/Oblique Angle Triangle | Properties of TriangleĪ triangle that has one angle that measures more than 90° is an obtuse angle triangle.

Vice versa, we can say that if a triangle satisfies the Pythagoras condition, then it is a right-angled triangle. considering the above right-angled triangle ACB, we can say: In a right-angled triangle, the sum of squares of the perpendicular sides is equal to the square of the hypotenuse.įor e.g. The side opposite to the right angle is the largest side of the triangle and is called the hypotenuse.The other two angles of a right-angle triangle are acute angles.Right-Angle TriangleĪ triangle that has one angle that measures exactly 90° is a right-angle triangle. Given below is an example of an acute angle triangle. So, all the angles of an acute angle triangle are called acute angles.Let’s look into the six types of triangles in detail:Ī triangle that has all three angles less than 90° is an acute angle triangle. Classification according to the length of its sides (Equilateral, Isosceles, Scalene).Classification according to internal angles (Right, Acute, Oblique).since congruent angles are angles of equal measure.Triangles can be classified in 2 major ways:.We have established that the rays forming these angles coincide under a reflection. The reflection of ∠ CAB will have the same measure as ∠ CBA since reflections preserve angle measure.The reflections of and the reflection of.The reflection of A is B since reflections preserve length and the segments share point C.The reflection of will have the same length as that of.Since these angles are equal in measure, the reflection of ray (side of the ∠) will coincide with its image.Since m∠ACD = m∠BCD and reflections preserve angle measure, the image of ∠ ACD will be the same measure as ∠ BCD.Under a reflection in, the reflection of C will be C, since C lies on the line of.m∠ACD = m∠BCD because an angle bisector forms two congruent angles which have equal measure.Label the intersection with the base as D. Construct an auxiliary line through point C bisecting ∠ C.